Introduction

Write a function to connect all the adjacent nodes at the same level in a binary tree.

Input Tree
       A
      / \
     B   C
    / \   \
   D   E   F


Output Tree
       A--->NULL
      / \
     B-->C-->NULL
    / \   \
   D-->E-->F-->NULL

Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Approach

The suggested approach is to use the Level Order Traversal and set the next pointer.

/*
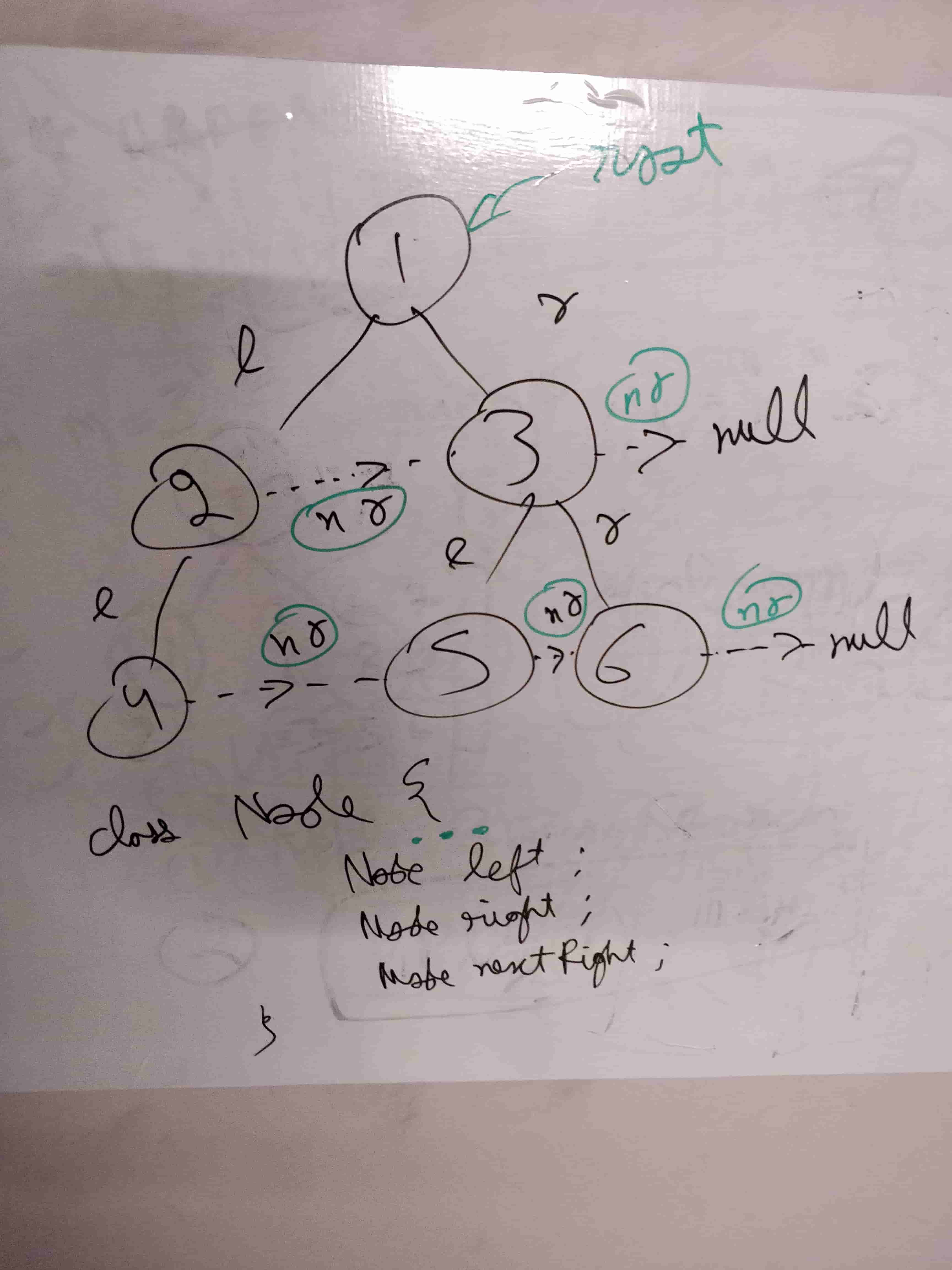
// Definition for a Node.
public class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
}
*/

public class Solution {
    public Node Connect(Node root) {
        if (root == null) {
            return root;
        }
        Queue<Node> q = new Queue<Node>();
        if (root.left != null) {
            q.Enqueue (root.left);
        }
        if (root.right != null) {
            q.Enqueue (root.right);
        }
        
        Node curr = null;
        // Level order traversal
        while (q.Count > 0) {
            var qCount = q.Count;
            while (qCount-- > 0) {
                var prev = curr;
                curr = q.Dequeue();
                // Connect prev with curr
                if (prev != null) {
                    prev.next = curr;
                }
                
                // Enqueue Left
                if (curr.left != null) {
                    q.Enqueue(curr.left);
                }
                // Enqueue Right
                if (curr.right != null) {
                    q.Enqueue(curr.right);
                }
            }
            // Reset for the level
            curr = null;
        }
        return root;
    }
}