Introduction

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

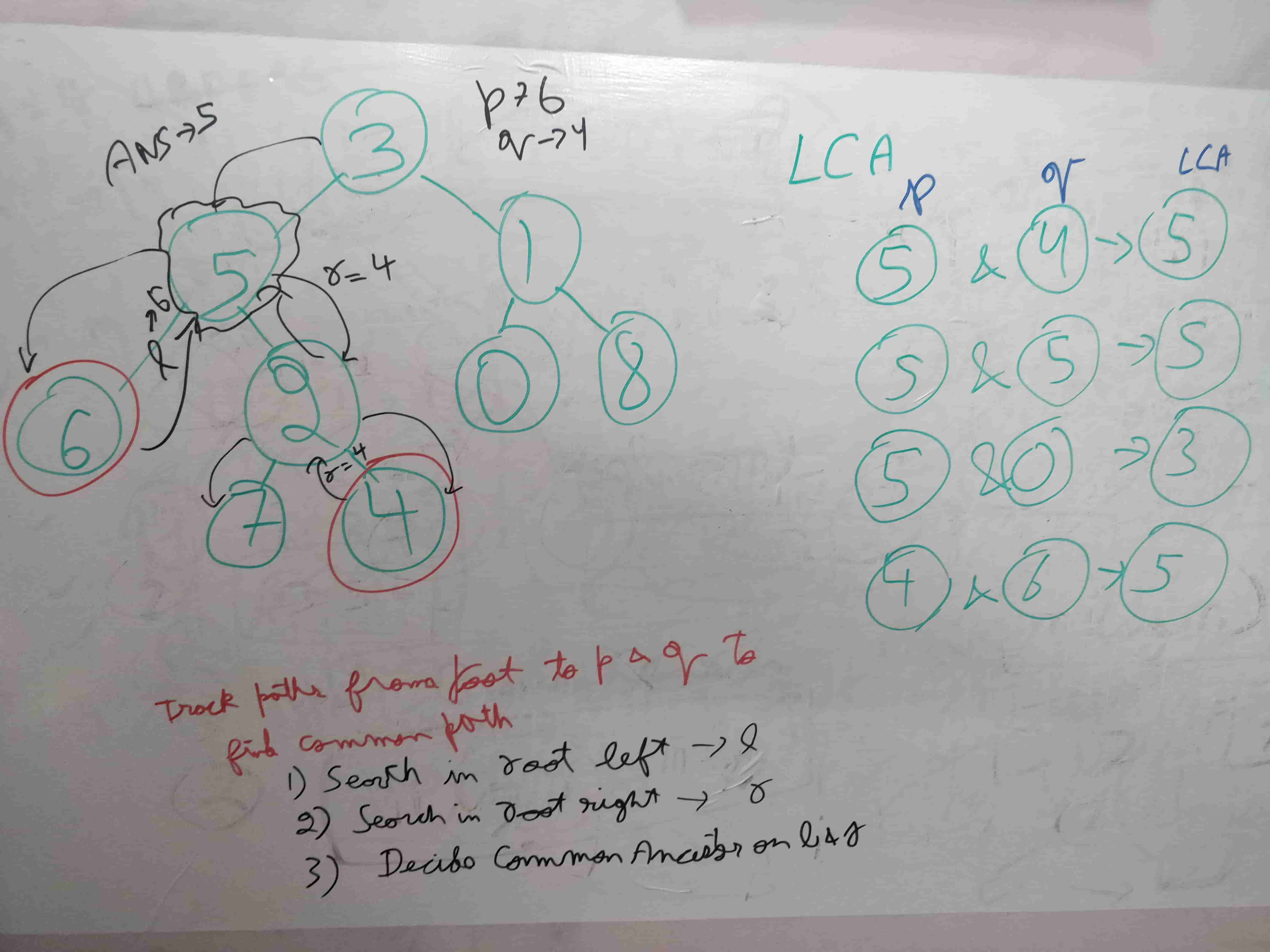
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Sample Example
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Approach

First the given nodes p and q are to be searched in a binary tree and then their lowest common ancestor is to be found. We can resort to a normal tree traversal to search for the two nodes. Once we reach the desired nodes p and q, we can backtrack and find the lowest common ancestor.

Approach Flow diagram
Sample Code for the problem using Recursion
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public TreeNode LowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || p == root || q == root) {
            return root;
        } 
        var l = LowestCommonAncestor(root.left, p, q);
        var r = LowestCommonAncestor(root.right, p, q);
        return l == null ? r : r == null ? l : root;
    }
}
C# Program using Recursion

Complexity Analysis

Time Complexity:
O(N), where N is the number of nodes in the binary tree. In the worst case we might be visiting all the nodes of the binary tree.

Space Complexity:
O(N). This is because the maximum amount of space utilized by the recursion stack would be N since the height of a skewed binary tree could be N.