Introduction

Consider a matrix with N rows and M columns, where each cell contains either a ‘0’ or a ‘1’ and any cell containing a 1 is called a filled cell. Two cells are said to be connected if they are adjacent to each other horizontally, vertically, or diagonally. If one or more filled cells are also connected, they form a region. find the length of the largest region.

Input 1:
1 1 0
0 0 1
1 0 1

Output 1:
4

Explanation 1:
In the above example, there are 2 regions one with length 1 and the other as 4. So largest region: 4

Input 2:
0 0 1 1 0
1 0 1 1 0
0 1 0 0 0
0 0 0 0 1

Output 2:
6

Explanation 2:
In the above example, there are 2 regions one with length 1 and the other as 6. So largest region: 6

Example Inputs

Approach

The first approach that comes to my mind after hearing this problem is Union Find algorithm which is discussed in detail below.

Union Find

Union-Find is a data structure that is capable of tracking and merging of disjoint sets.

Operations

Add (i)
Makes a new set with i as its only element.
Union (i, j)
Combines the set to which i belongs and the set to which j belongs.

Note:
We have not explained the additional operations like Find, Count, Size.

Example

Let’s take an example. Let’s say that a set of A = 3, 4 is already created. In this case, the first entry element, 3, becomes the root node, and 3 is the value representing A. It is as follows.

Let’s say we have another set, B = 1,2. When joining A and B, root nodes are connected as follows

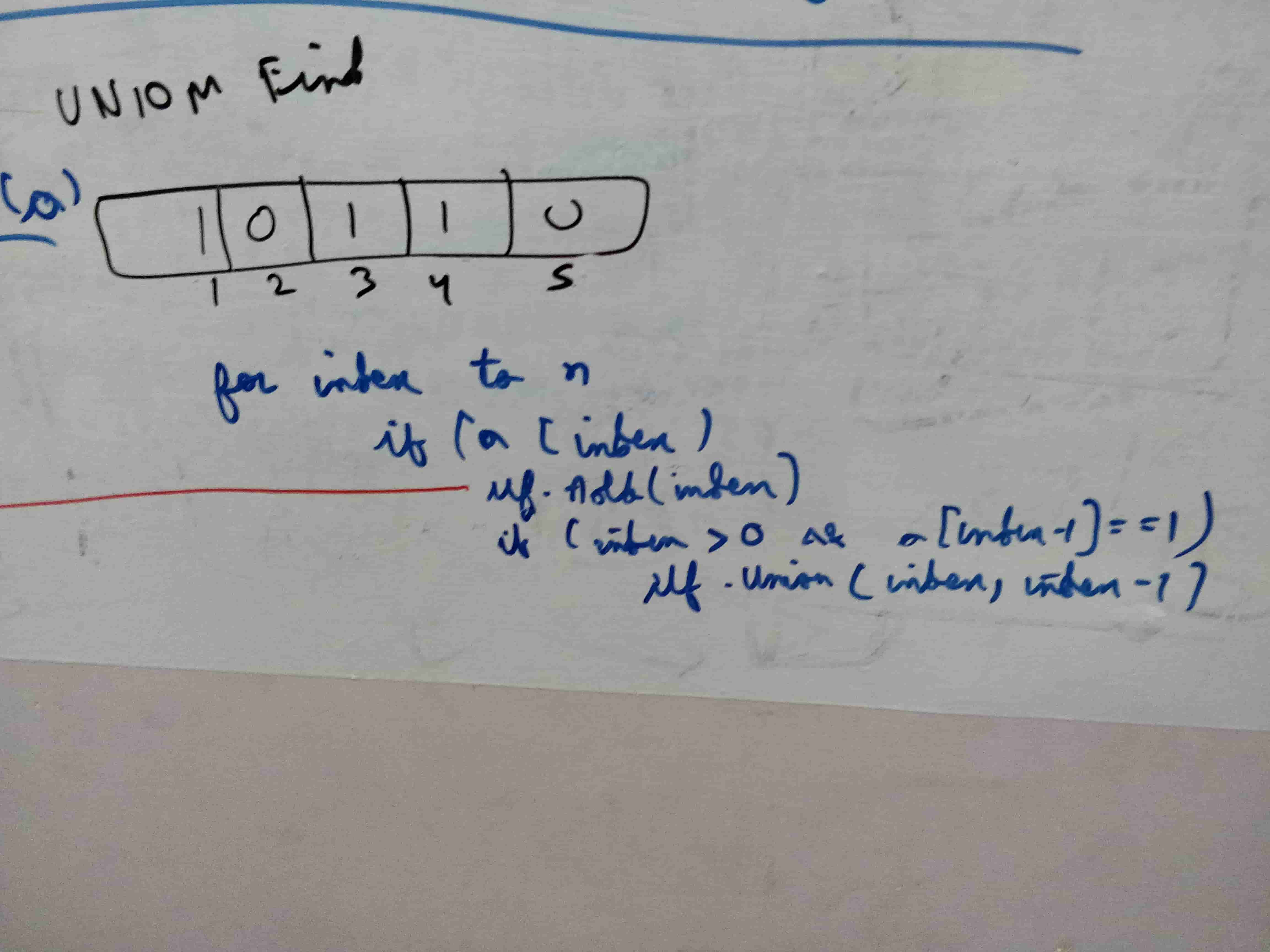
Union Find Operation

The array a has value set at the indices 1, 3, 4. The union find operation for the 1-D array corresponds to the add operation and the union operation by checking the last index value.

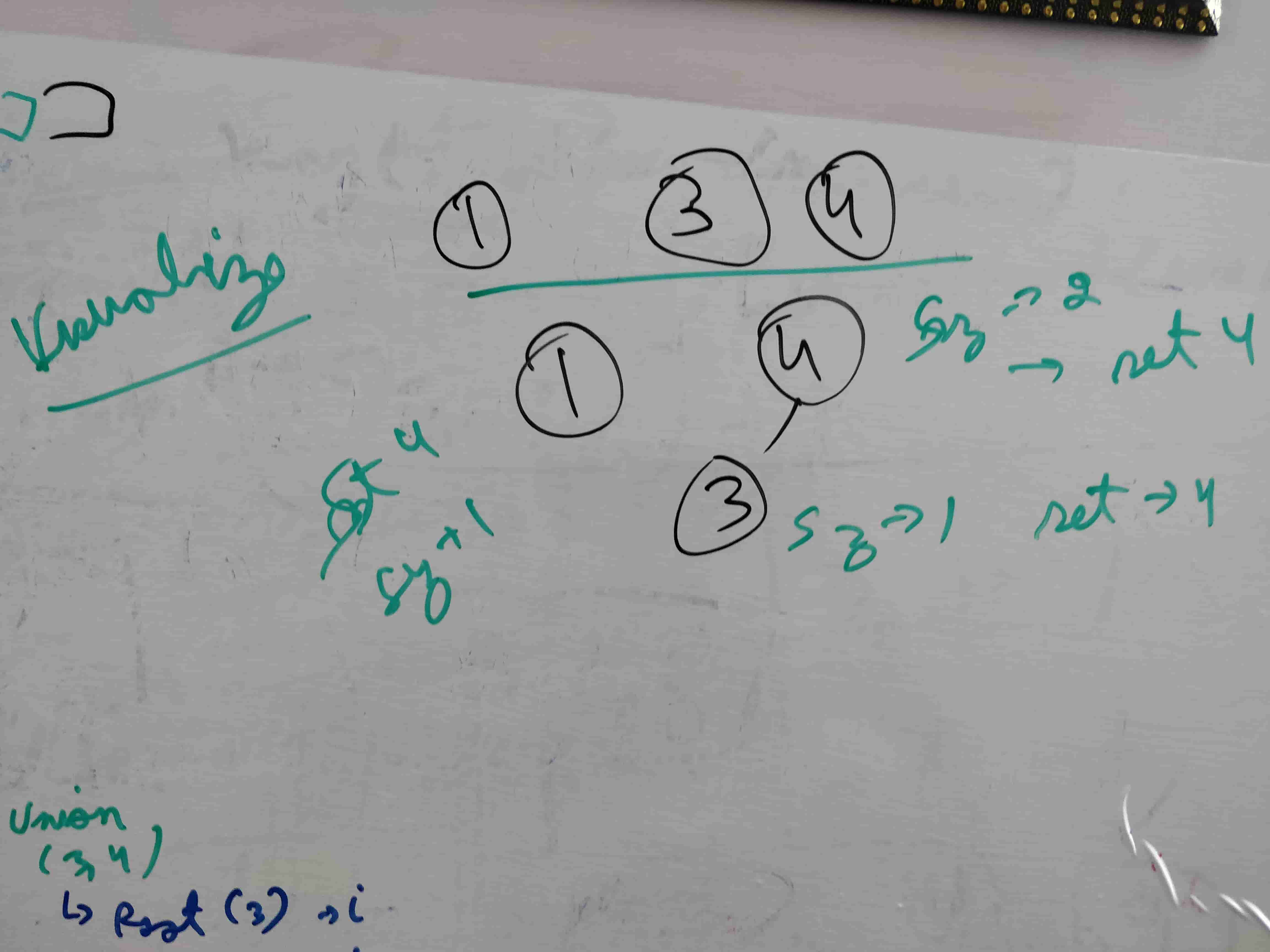
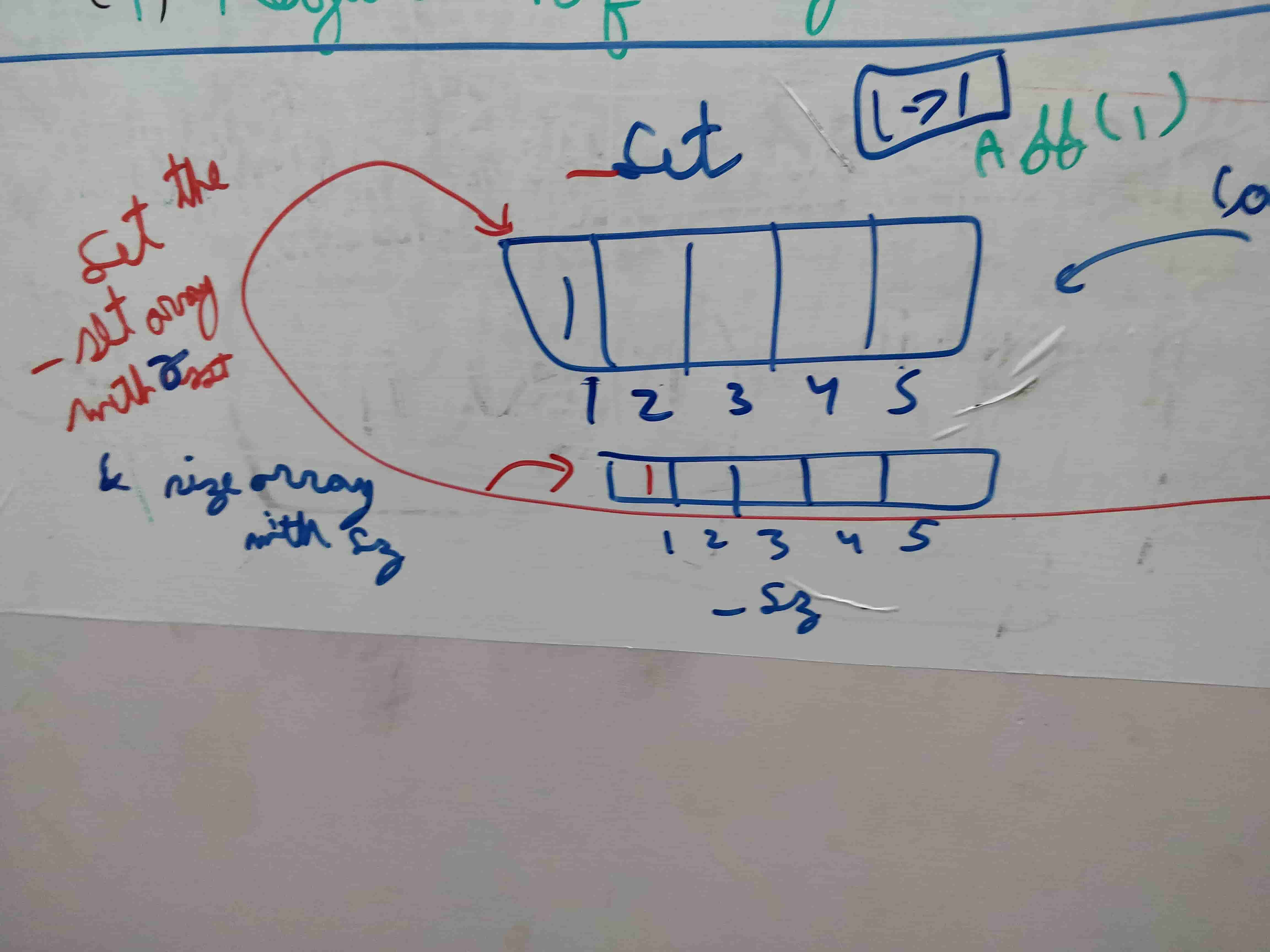
Visualization for the Union Find with Size

Add Operation

Adds the index to the set array which denotes the root and sets the size array to 1.

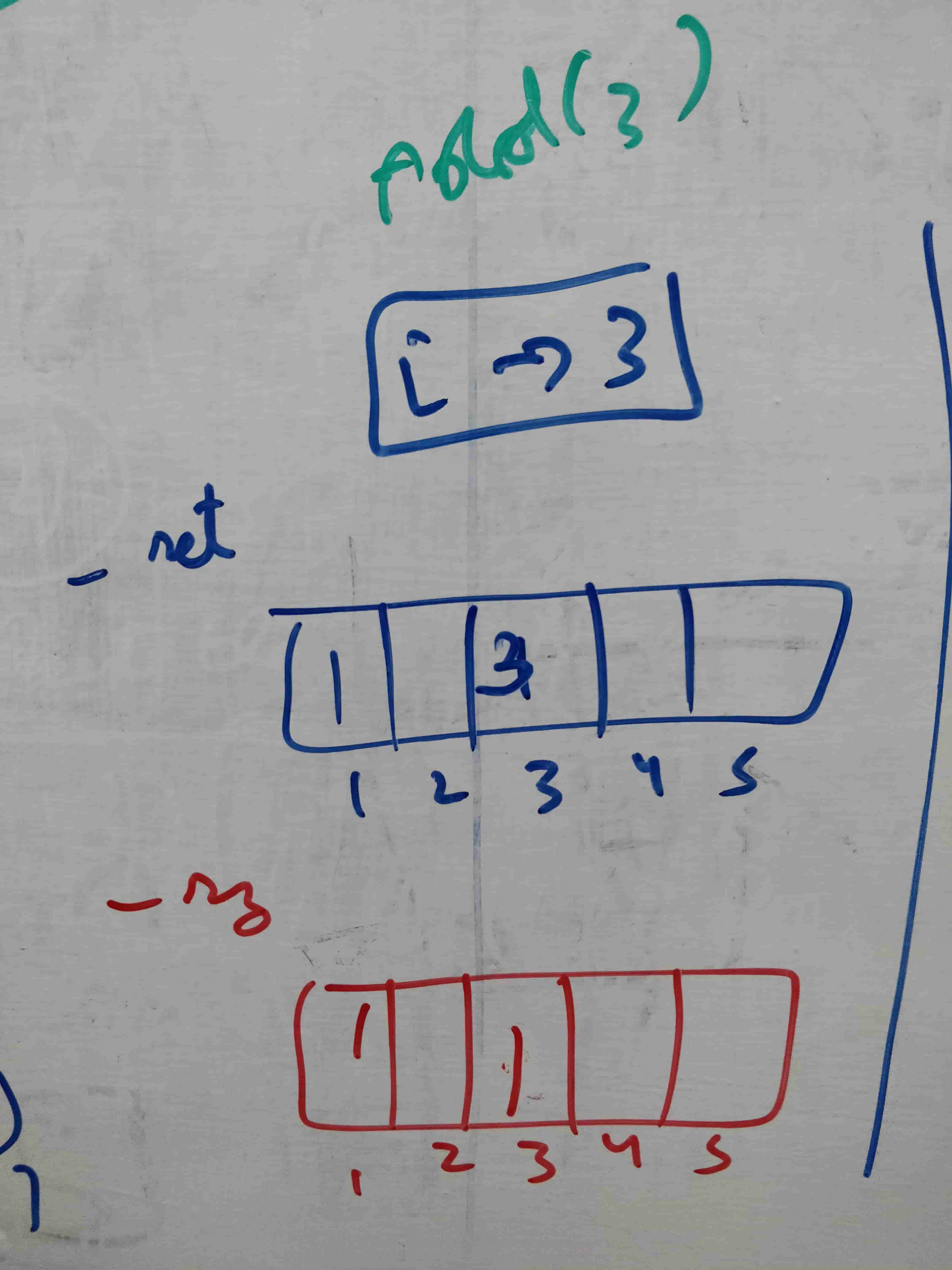
Union operation

When combining any two sets, it is efficient to combine sets with fewer elements into many sets of subtrees.

Union by Size
In order to improve effficiency we track the size of the sets and merge smaller one to the larger one.

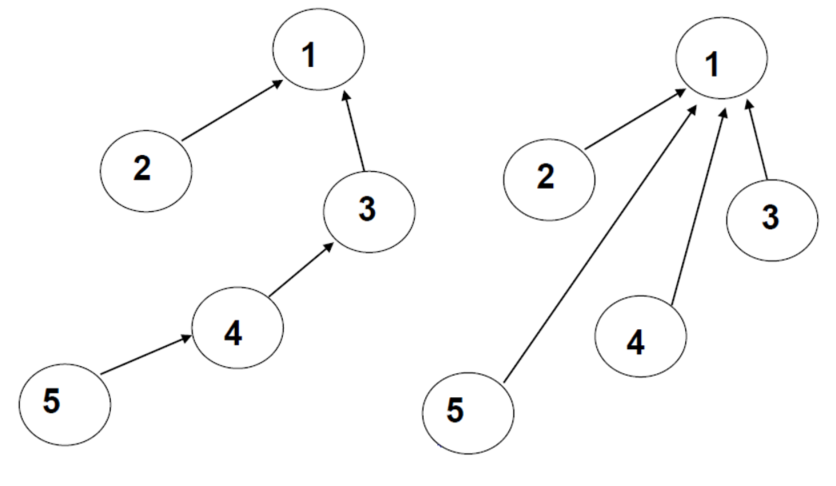
Path Compression

The path compression is to make all nodes point to the root as follows:
S stores the root node instead of the parent node index. When you perform a find operation, you need to go back as far as the height of the tree to find the root node.

Once you perform path compression, you can reduce the computational complexity of the find operation that finds the root node.

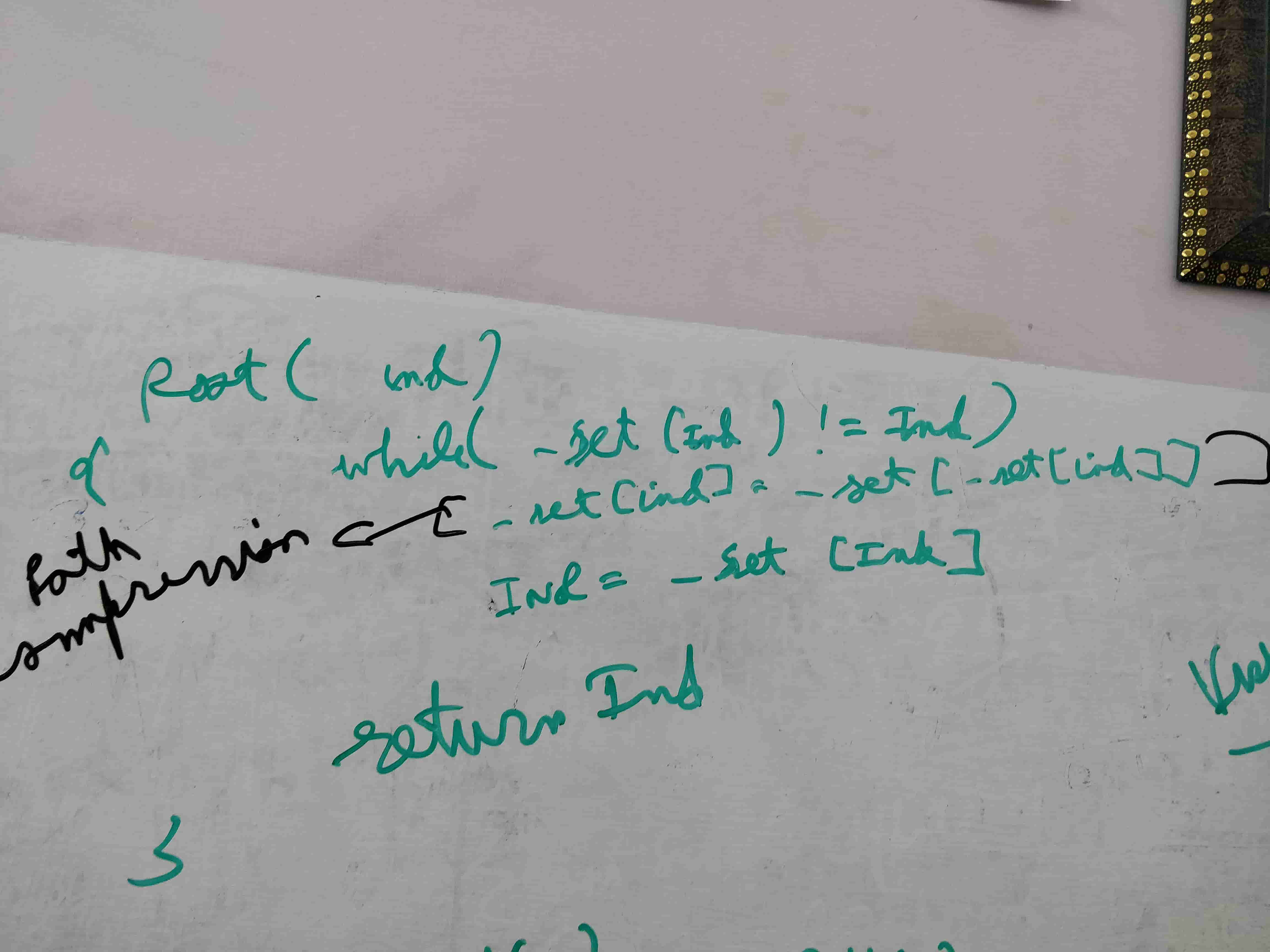
Code Changes for adding path compression

Program

using System;
using System.Linq;
public class GFG {
    private class UnionFind
    {
        private readonly int[] _set;
        private readonly int[] _sz;

        public UnionFind(int n)
        {
            _set = new int[n + 1];
            _sz = new int[n + 1];
        }

        public void Add(int index)
        {
            _set[index] = index;
            _sz[index] = 1;
        }

        private int Root(int index)
        {
            while (index != _set[index])
            {
                // Path Compression
                _set[index] = _set[_set[index]];
                index = _set[index];
            }
            return index;
        }

        public int Union(int i, int j)
        {
            i = Root(i);
            j = Root(j);
            if(i == j) {
                return _sz[i];
            }
            if (_sz[i] < _sz[j])
            {
                _set[i] = j;
                _sz[j] += _sz[i];
                return _sz[j];
            }

            _set[j] = i;
            _sz[i] += _sz[j];
            return _sz[i];
        }
    }

    private static int FindLargestRegion(int[] arr, int m, int n)
    {
        if (arr.Length == 0)
        {
            return 0;
        }
        var uf = new UnionFind(arr.Length);
        var max = 0;
        for (var i = 0; i < n; i++)
        {
            for (var j = 0; j < m; j++)
            {
                var arrIndex = i * m + j;
                if (arr[arrIndex] == 0)
                {
                    continue;
                }

                max = Math.Max(max, 1);

                // index of the current element
                var index = arrIndex + 1;
                uf.Add(index);

                // left element in same row
                var leftIndex = index - 1;
                if (leftIndex > 0 && leftIndex % m > 0 && arr[leftIndex - 1] == 1)
                {
                    max = Math.Max(max, uf.Union(index, leftIndex));
                }
                // left diagonal in above row
                var leftDiagIndex = index - m - 1;
                if (leftDiagIndex > 0 && leftDiagIndex % m > 0 && arr[leftDiagIndex - 1] == 1)
                {
                    max = Math.Max(max, uf.Union(index, leftDiagIndex));
                }
                // right diagonal in above row
                var rightDiagIndex = index - m + 1;
                if (rightDiagIndex > 0 && index % m > 0 && arr[rightDiagIndex - 1] == 1)
                {
                    max = Math.Max(max, uf.Union(index, rightDiagIndex));
                }

                // top in above row
                var aboveIndex = index - m;
                if (aboveIndex > 0 && arr[aboveIndex - 1] == 1)
                {
                    max = Math.Max(max, uf.Union(index, aboveIndex));
                }
            }
        }
        return max;
    }

    public static void Main()
    {
        var t = int.Parse(Console.ReadLine() ?? "0");
        while (t-- > 0)
        {
            var mn = Console.ReadLine()?.Split(" ");
            if (mn != null)
            {
                var n = int.Parse(mn[0]);
                var m = int.Parse(mn[1]);
                var arr = Console.ReadLine()?.Split(" ", StringSplitOptions.RemoveEmptyEntries).Select(int.Parse).ToArray();
                Console.WriteLine(FindLargestRegion(arr, m, n));
            }
        }
    }
    
}