Introduction
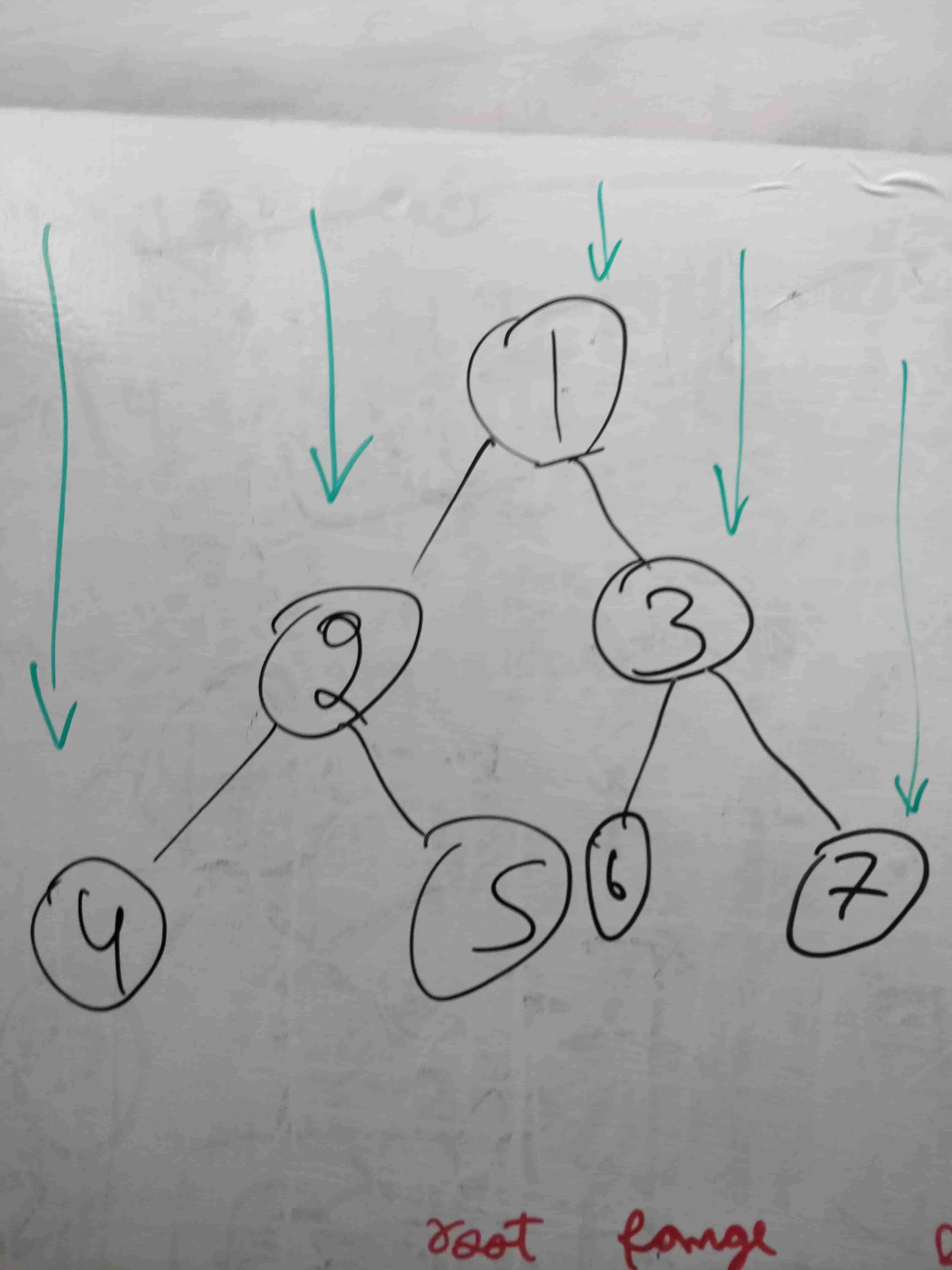
Given below is a binary tree. The task is to print the top view of binary tree. Top view of a binary tree is the set of nodes visible when the tree is viewed from the top. For the given below tree
1
/ \
2 3
/ \ / \
4 5 6 7
Top view will be: 4 2 1 3 7
Note: Print from leftmost node to rightmost node.Approach
One idea can be do a level order traversal with the range and storing the data for the range in the map that comes first. Other can be to store the track of range and depth during traversal along with map.
The idea is to create a map keyed on the range (horizontal distance from root). We add or update if the depth is less than the current stored element.

/*class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}*/
class Node2 {
public Node2(int depth, int data) {
this.depth = depth;
this.data = data;
}
public int depth;
public int data;
}
class View
{
// function should print the topView of the binary tree
static void topView(Node root)
{
SortedMap<Integer, Node2> map = new TreeMap<Integer, Node2>();
// add your code
topViewHelper(root, 0, 0, map);
String res = "";
// Traversing through the map
for (SortedMap.Entry<Integer, Node2> me : map.entrySet()) {
res += me.getValue().data + " ";
}
System.out.println(res.trim());
}
private static void topViewHelper(Node root, int range, int depth, SortedMap<Integer, Node2> map) {
if (root == null) {
return;
}
if (!map.containsKey(range)) {
Node2 node2 = new Node2 (depth, root.data);
map.put(range, node2);
} else if (depth < map.get(range).depth) {
Node2 node2 = new Node2 (depth, root.data);
map.put(range, node2);
}
topViewHelper(root.left, range - 1, depth + 1, map);
topViewHelper(root.right, range + 1, depth + 1, map);
}
}References
Top View of Binary Tree | Practice | GeeksforGeeks
Given below is a binary tree. The task is to print the top view of binary tree. Top view of a binary tree is the set of nodes visible when the tree is viewed from the top. For the given below tree 1 &



