Introduction
This problem is part of the May 2020 monthly challenge on the LeetCode platform.
We write the integers of A and B (in the order they are given) on two separate horizontal lines. Now, we may draw connecting lines: a straight line connecting two numbers A[i] and B[j] such that:
- A[i] == B[j];
- The line we draw does not intersect any other connecting (non-horizontal) line.
Note that connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.
Return the maximum number of connecting lines we can draw in this way.
Example 1:
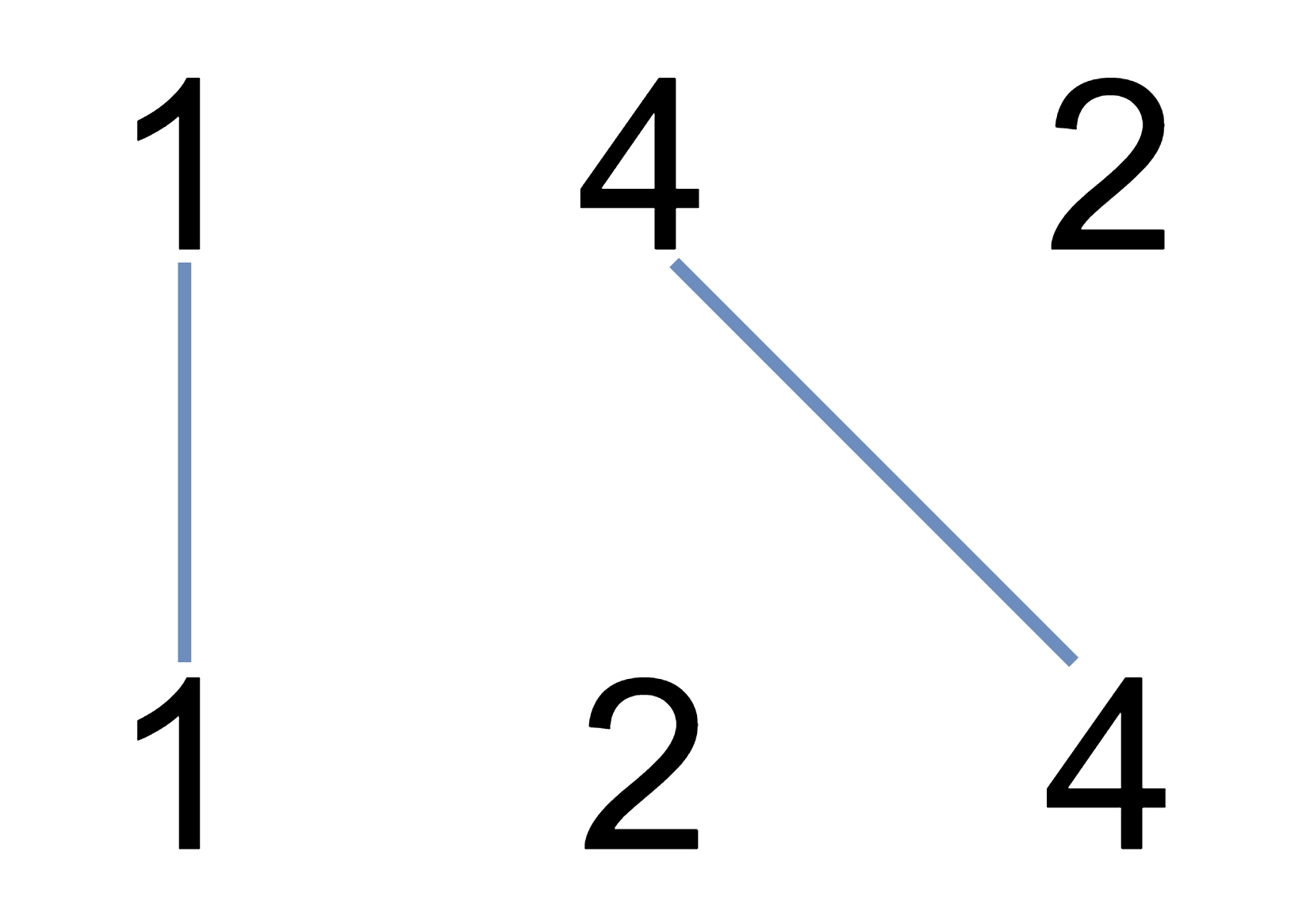
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.
Approach
Given the Inputs A and B, we draw out the matrix and map the non-intersecting lines. Let's observe and find a pattern in the below matrix diagram. I had laid the matrix diagram in such a way that the column matrix denotes B [1, 4, 2] and rows denote [1, 2, 4].
We go over the elements one by one, first assuming that only a single element present in A [1, 2, 4] which is element 1 and calculate the number of non- intersecting lines, and repeat the case for elements 1 and 2, finally 1, 2 and 3.
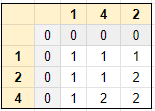
| Row # | Col # | A | B | # Non-Intersecting | Comments | |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | same elements | |
| 0 | 1 | 1 | 4 | 1 | no change | |
| 0 | 2 | 1 | 2 | 1 | no change | |
| 1 | 0 | 2 | 1 | 1 | no change | |
| 1 | 1 | 2 | 4 | 1 | no change | |
| 1 | 2 | 2 | 2 | 2 | same elements | |
| 2 | 0 | 4 | 1 | 1 | no change | |
| 2 | 1 | 4 | 4 | 2 | no change | |
| 2 | 2 | 4 | 2 | 2 | same elements |
We see below two patterns forming in the above matrix diagram:
1. Same elements in A and B:
We see that the same elements for row and col follow the below pattern:
Matrix [ Row, Col ] = Matrix [ Row - 1, Col - 1 ] + 1
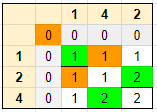
| Row # | Col # | A | B | # Non-Intersecting | Comments | |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | = 1 + 0 | |
| 1 | 2 | 2 | 2 | 2 | = 1 + 1 | |
| 2 | 2 | 4 | 2 | 2 | = 1 + 1 |
2. Different elements in A and B
We see that the different elements for row and col follow the below pattern:
Matrix [ Row, Col ] = MAX ( Matrix [ Row - 1, Col ], Matrix [ Row, Col - 1 ]) + 1
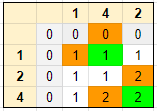
| Row # | Col # | A | B | # Non-Intersecting | Comments | |
|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 4 | 1 | = MAX (1, 0) | |
| 0 | 2 | 1 | 2 | 1 | = MAX (1, 0) | |
| 1 | 0 | 2 | 1 | 1 | = MAX (0, 1) | |
| 1 | 1 | 2 | 4 | 1 | = MAX (1, 1) | |
| 2 | 0 | 4 | 1 | 1 | = MAX (0, 1) | |
| 2 | 1 | 4 | 4 | 2 | = MAX (2, 2) |
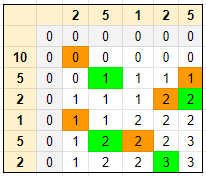
Example 2
Also, let us follow the below example and try to identify the pattern. I have highlighted the common patterns.
We traverse the matrix row-wise and try to apply the two patterns that we have identified with the first example.
- Same elements: Add one to prior diagonal element
- Different elements: Choose the maximum of the adjacent top and left elements
Code
I have coded the above approach in the C# code.
using System;
namespace LeetCode.Monthly_Challenge.May_2020
{
public class MaxCrossedLines
{
public static void Run()
{
var mc = new MaxCrossedLines();
Console.WriteLine(mc.MaxUncrossedLines(new[] { 1, 4, 2 }, new[] { 1, 2, 4 }));
Console.WriteLine(mc.MaxUncrossedLines(new[] { 2, 5, 1, 2, 5 }, new[] { 10, 5, 2, 1, 5, 2 }));
Console.WriteLine(mc.MaxUncrossedLines(new[] { 1, 3, 7, 1, 7, 5 }, new[] { 21, 9, 2, 5, 1 }));
Console.WriteLine(mc.MaxUncrossedLines(new[] { 1, 3, 7, 1, 7, 5 }, new[] { 1, 9, 2, 5, 1 }));
}
public int MaxUncrossedLines(int[] A, int[] B)
{
var prevResults = new int[A.Length + 1, B.Length + 1];
for (var i = 0; i < A.Length; i++)
{
for (var j = 0; j < B.Length; j++)
{
if (A[i] == B[j])
{
prevResults[i + 1, j + 1] = 1 + prevResults[i, j];
}
else
{
prevResults[i + 1, j + 1] = Math.Max(prevResults[i, j + 1], prevResults[i + 1, j]);
}
}
}
return prevResults[A.Length, B.Length];
}
}
}
Conclusion
The mentioned problem is an example of how drawing out the cases might help even to reach the solution. In this case, when we draw out the matrix, we see the two patterns visible.
Complexity: O(mn)
Approach for Thought
I thought another alternate Non-DP approach one could pursue to achieve similar results.
- We get the list of indexes of the A's element find in B.
A = [ 1, 3, 7, 1, 7, 5 ]
B = [ 1, 9, 2, 5, 1 ]
I = [ [0, 4], [0, 4], [ 3] ]
Element 1 in A is found at two indexes 0 and 4
Element 5 in A is found at one index 3 - We repeat and try to form a pattern from left to right in increasing order. (alternatively, from right to left in decreasing order also works)
Orders 1 = 0, 4
Orders 2 = 0, 3 - We get the max size 2 for the above case.

