Introduction
A graph is a data structure represented by a set of vertices and edges G = (V, E). A vertex in a graph is called an articulation point or a cut vertex iff removing it disconnects the graph. It identifies the vulnerabilities in a connected network, on failure would split the graph. They are useful for designing reliable networks. Following are examples of the articulation point highlighted in red.
Interesting Fact
Jeffery Westbrook and Robert Tarjan developed an efficient data structure for this problem. Tarjan is known for his pioneering work on graph theory algorithms and data structures (least common ancestors algorithm and strongly connected components algorithm)
Depth-first Search and Classification of Edges
The idea is to use DFS (depth-first search), it suggests to traverse more in-depth into the graph whenever possible.
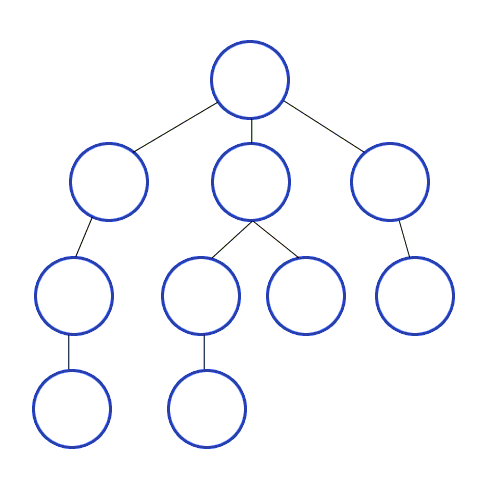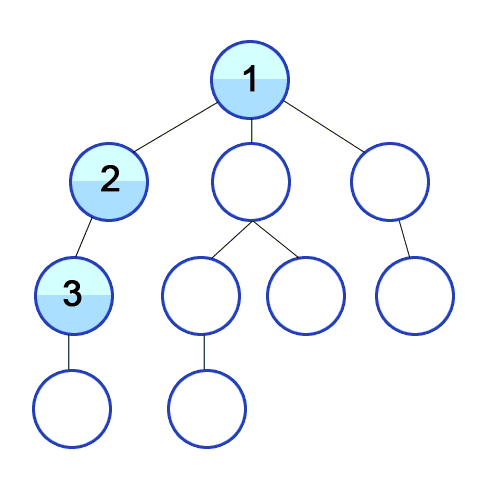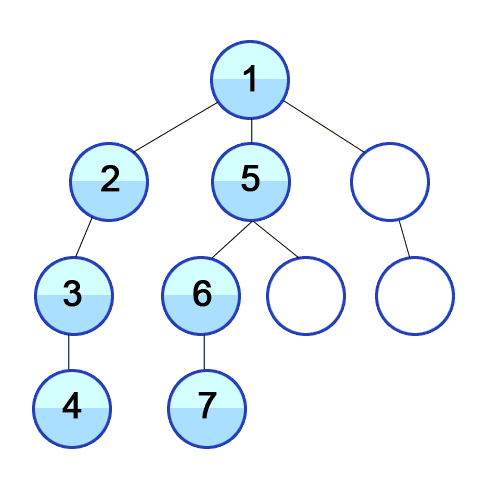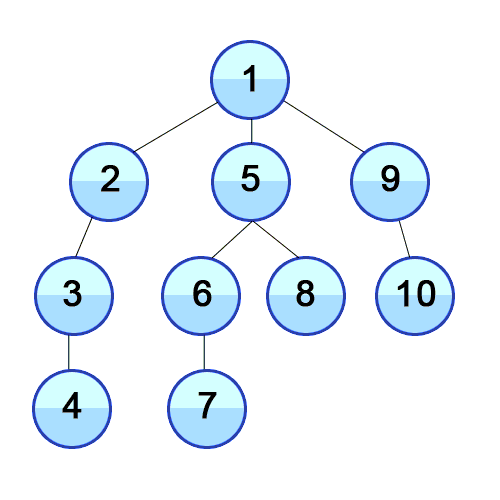
Another attractive property of the depth-first search is that the search can be used to classify the edges of the input graph G = (V, E).
- Tree edges would be those edges (u, v) if 'v' were first discovered by exploring edge (u, v).
- Forward edges are those nontree edges (u, v) connecting a vertex 'u' to a descendant v in a depth-first tree.
- Back edges are those edges (u, v) connecting a vertex 'u' to an ancestor v in a
depth-first tree. Self-loops, which may occur in directed graphs, are considered
to be back edges. - Cross edges are all other edges. They can go between vertices in the same
depth-first tree, as long as one vertex is not an ancestor of the other, or they can go between vertices in different depth-first trees.
Below image discusses the progress of the depth-first-search algorithm DFS on a directed graph. As the algorithm explores edges, they are shown as either shaded (if they are tree edges) or dashed (otherwise). Nontree edges are labelled B, C, or F according to whether they are back, cross, or forward edges. We timestamped the Vertices by discovery time/finishing time.
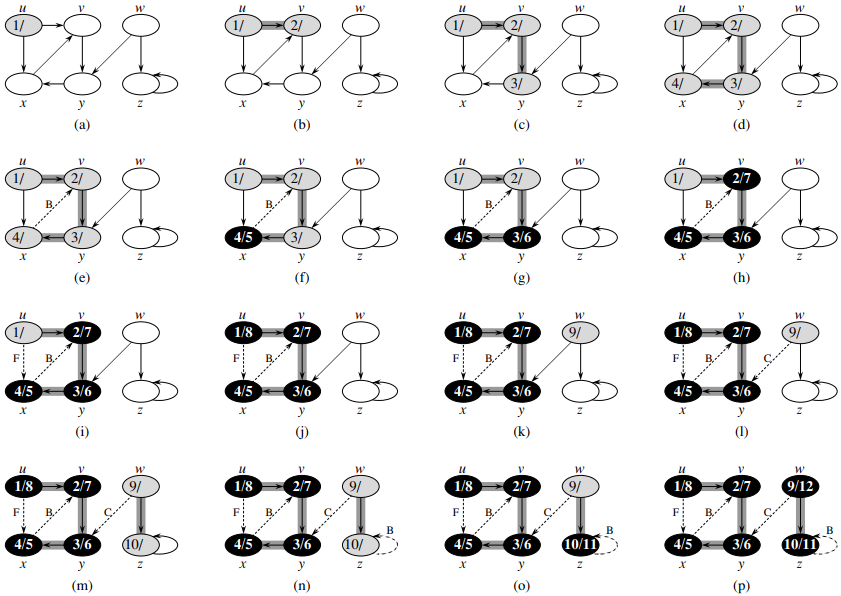
Algorithm
The idea is to identify the articulation point using the classification of edges using DFS.
We use below stores to identify the articulation points
V -> store the visited element
D -> stores the discovery times of visited vertices
L - store the low times of each node
P -> stores parent vertices in DFS tree
Ap -> stores the articulation points
A vertex u is an articulation point if
1. u is the root of the tree, and it has at least two children
(removing root result in disconnected graph and consider root denotes the start of the DFS)
Approach
maintain a parent array P for vertices
P -> stores parent vertices in DFS tree
Condition in the code
if( P[u] == null && children > 1)
2. u is not the root of the tree, and it has a child v such that there is no back edge from v to one of the ancestors of 'u'
(the v child not reached from any ancestor of u)
Approach
maintain a discovery array D to store the discovery times of the vertices and maintain an array to store the low times of each node to identify the earliest visited vertex (the low time is initialized the same way as D and gets updated if any ancestor exists with lower low time)
D -> stores the discovery times of visited vertices
L - a map to store the low times of each node
Calculation to update the low time
L[u] = Math.Min(D[u], D[w])
where w is an ancestor of 'u' and there is a back edge from some descendant of u to w
Condition in the code
if( P[u] != null && L[u] >= D[u])
Pseudo Code
FindArticulationPoint(Graph graph) {
// Initialize list of Visited, Discovery, Low time,
// Parent and Articulation Points
Initialize V, D, L, P, Ap
// set first vertex
Let v = graph.FirstVertex();
// mark initial discovery time
Let t = 0;
// Perform Depth-first search and populate Ap Articulation points
Dfs(V, Ap, v, D, L, P, t);
return Ap;
}
Dfs(V, Ap, v, D, L, P, t) {
// Mark visited
V.Add(v)
// add discovery time and low time
D.Add(t)
L.Add(t)
t++;
Let children = 0
Let isAp = false
foreach(adjV in v.getAdjacentVertices) {
// ignore if adjacent vertex is the parent (already visited)
if(adjV == P[v]) {
continue;
}
// if not already visited, visit it
if(!V[adjV]) {
P[adjV] = v;
children++;
// Dfs on adjacent vertex
Dfs(V, Ap, adjV, D, L, P, t);
// update isAp if low time of adjacent vertex is
// greater than the discovery time of the vertex
if(L[adjV] >= D[v]) {
// denotes that no ancestor or backedge to already visit
isAp = true;
} else {
// update the low time
L[v] = Math.Min(L[v], L[adjV]);
}
} // if adjacent vertex is already visited
else {
// if adjacent vertex already visited, update the low time if required
L[v] = Math.Min(L[v], L[adjV]);
}
}
//checks if either conditions is yes, it is articulation point
// condition 1 - root of the tree and atleast two children or
// condition 2 - not the root and no backedge to ancestor
if((P[v] == null && children >= 2) || P[v] != null && isAp ) {
Ap.Add(v);
}
}
Demo
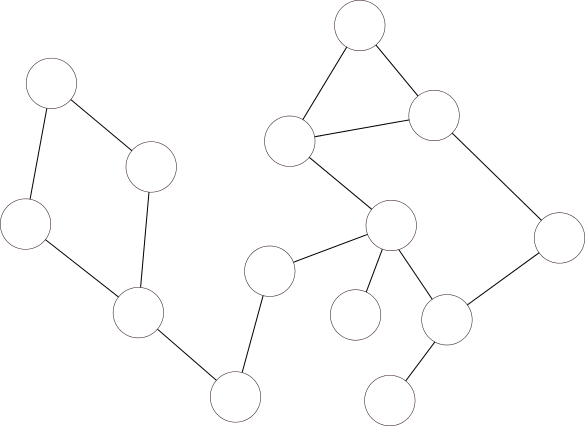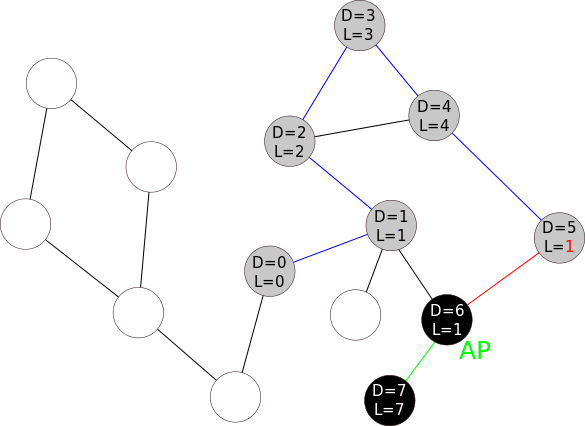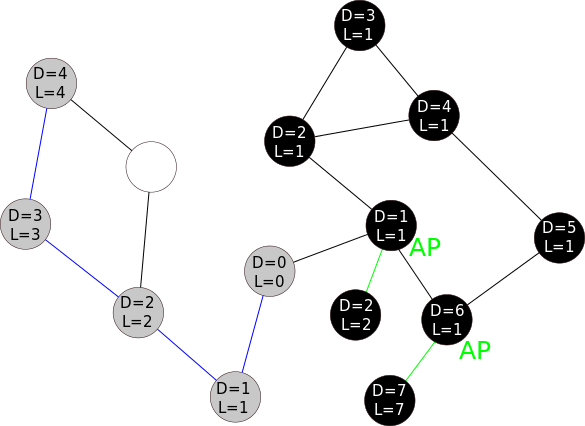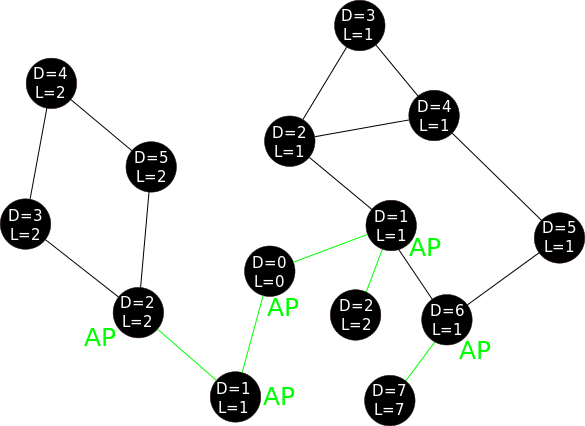
References
- https://www.geeksforgeeks.org/articulation-points-or-cut-vertices-in-a-graph/
- Introduction to Algorithms by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein
- https://en.wikipedia.org/wiki/Robert_Tarjan
- https://en.wikipedia.org/wiki/Biconnected_component
- https://brilliant.org/wiki/depth-first-search-dfs/
- https://en.wikipedia.org/wiki/Depth-first_search
- https://www.youtube.com/watch?v=2kREIkF9UAs
- https://github.com/mission-peace/interview/blob/master/src/com/interview/graph/ArticulationPoint.java



